カテキヨースタッフより！

2024年10月26日

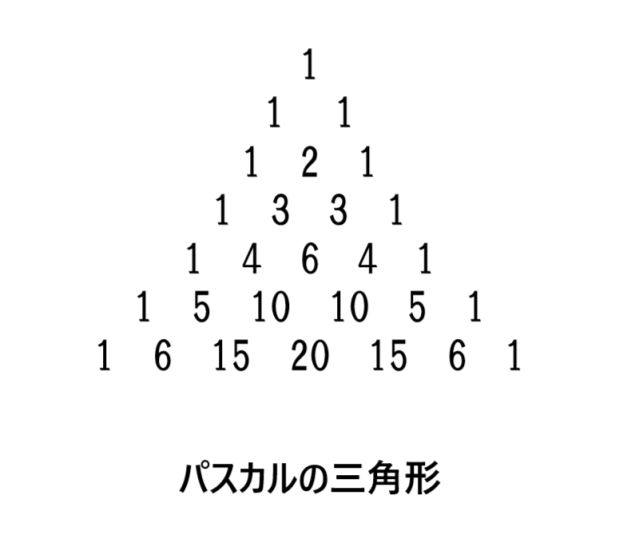
【高校数学】パスカルの三角形【二項定理】

青森市の皆さんこんにちは、昨日の記事で11の倍数についての話が出ましたので、今日はパスカルの三角形について話してみようと思います。
パスカルの三角形と11のｎ乗の関係についてはさらに次回に書きたいと思います。

パスカルの三角形は高校数学で言えば数Ⅱの分野『式と証明』の二項定理と関わりがあります。

二項定理は
(x + y)ⁿ = _nC₀xⁿy⁰ + _nC₁x^n-1y + _nC₂x^n-2y² + _nC₃x^n-3y³ + … + _nC_n-1xy^n-1 + _nC_nx⁰yⁿ
のことです。
２つの項のｎ乗を展開した際の公式になります。

パスカルの三角形（タイトルの図形）との関係については
図形上の各項の数値が二項定理の各項_nC_rと一致します。

n乗の係数と言われても最初は難しいと思いますので、例えば2乗の係数について考えます。

(x + y)² = x² + 2 xy + y²

は中学校で習う公式ですが、x²、xy、y²の係数は1 , 2 , 1です。
これは₂C₀ = 1、₂C₁ = 2 、₂C₂ = 1
と一致しています。

同様に３乗についてはパスカルの三角形上では

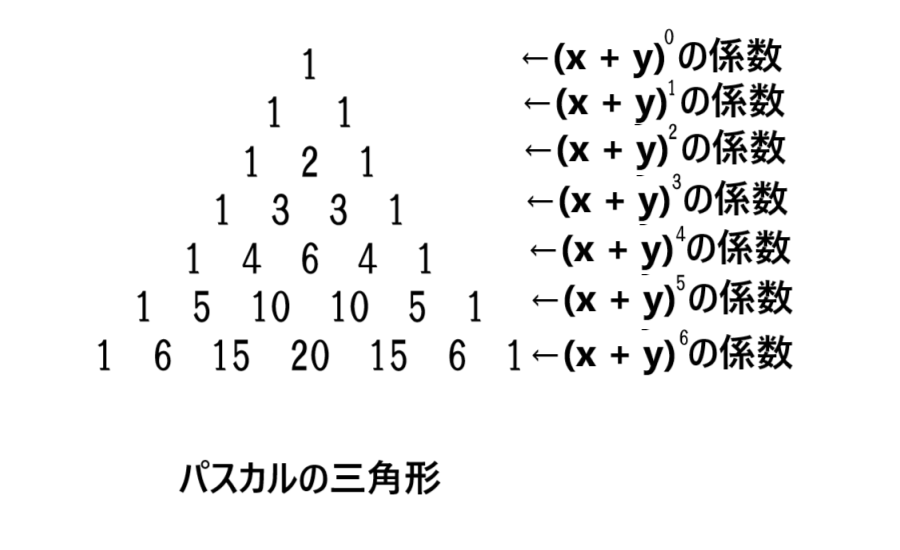
それぞれの係数が 1 , 3 , 3 , 1 と書いてありますが

(x + y)³ = x³ + 3 x²y + 3 xy² + y³

のそれぞれの項の係数と一致しているのが分かります。
また、 ₃C₀ = 1、₃C₁ = 3、 ₃C₂ = 3、₃C₃ = 1 とも一致していることが分かります。

次にパスカルの三角形の書き方についてお話しします。
まずは下の図を見てください。

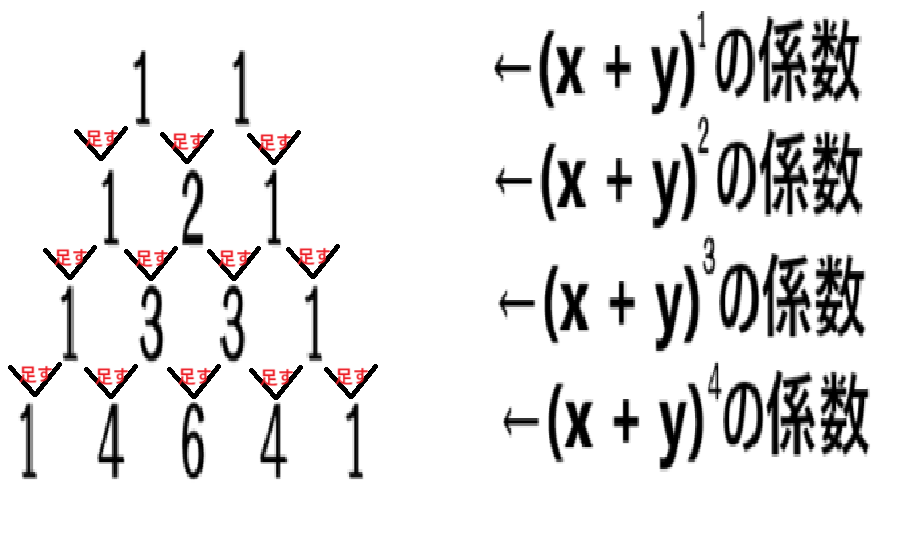
図のように「上の行の隣り合った数字を足し合わせたもの」を下の行に書いていきます。
数字と数字の間に書いていくのがコツです。
なにも数字が書いてないところ（左端、右端）は0だと思ってください。
これを繰り返していくと何乗でも作ることができます。
0乗については一番上に書けばよいです。（基本的に使わないので書かなくてもOK)

書き方を覚えるのは必須ですので、すぐに覚えてしまいましょう。

次回はパスカルの三角形と１１のｎ乗との関係についてお話しします。

青森市で、中学受験、高校受験、大学受験、受験予備校といえば、

"完全個別担任制"
KATEKYO学院　青森古川校
TEL　:　017-774-2277