2024年11月4日

【中学数学】柱を斜めに切ってできた立体の体積【裏技】

※この記事は2024.10.21に古川校のページにも書いた記事の再掲となります。

皆さんこんにちは、青森県家庭教師協会・ＫＡＴＥＫＹＯ青森です。


今日は高校入試でも出題されがちな立体を斜めに切った時にできる図形（断頭〇〇柱という）の体積について
裏技をお知らせします。

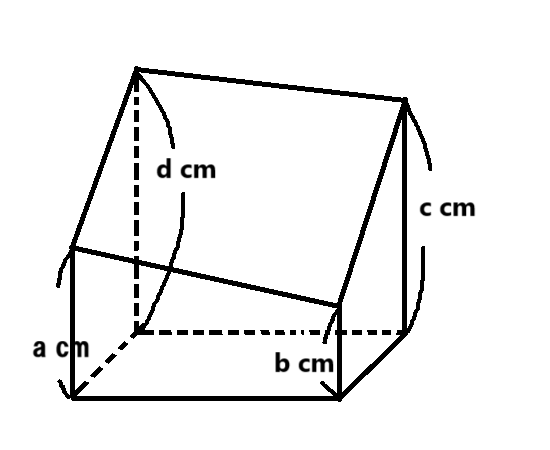
上の断頭四角柱の体積Ｖは底面積をＳとした際、次の公式が成り立ちます。


Ｖ　＝　Ｓ ×（a + b + c + d）÷ 4


（a + b + c + d）÷ 4　は高さの平均を出している式となります。
つまり体積は

(底面積) × (高さの平均)　で出すことができます。


この公式使って下の立体の体積を求めてみましょう。

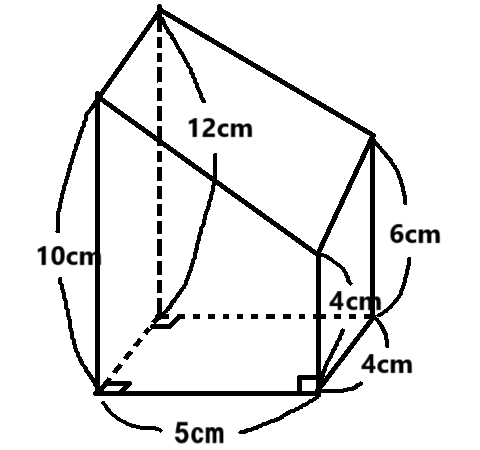
解）

Ｖ　＝　20 × (10 + 4 + 6 + 12) ÷ 4
　　＝　160

よって 160 cm³

となります。

この公式の良い所は
底面が四角形でなくても（三角形や円）、
１辺の高さに０が含まれても使えるところです。


例）
底面積が10cm²、高さがそれぞれ3cm,4cm,5cmの断頭三角柱の体積Ｖは

Ｖ　＝　10 × (3 + 4 + 5) ÷ 3
　　＝　40 cm³

底面積が16πcm²、高さが一番低い所が5cm、高い所が9cmである断頭円柱の体積Ｖは

Ｖ　＝　16π × (5 + 9) ÷ 2
　　＝　112π cm³

底面積が10cm²、高さがそれぞれ0cm,4cm,10cm,6cmの断頭四角柱の体積Ｖは

Ｖ　＝　10 × (0 + 4 + 10 + 6) ÷ 4
　　＝　50 cm³


となります。


この公式を覚えておけば5分かかるところを1分で解くことが出来るようになります。
いつでも使えるようにしておきましょう。


書いた人：青森事務局　大坂

青森県で中学受験、高校受験、大学受験、受験予備校といえばＫＡＴＥＫＹＯ学院！
学習相談は時期問わず、いつでもお受けしておりますので、
まずはこちらからご相談ください。